Aula Virtual Conalep Zamora: aind-uni1-tema5

1.3 Calcula el comportamiento de los cambios de la variable utilizando métodos numéricos.

A. Determina las condiciones de continuidad.

Introduce la definición de la diferencial
Curvaturas de las gráficas.
Análisis de raíces con división sintética
Interpretación de la curva analizando los cambios de signos.

B. Determinación de la continuidad de una función.

Condiciones de continuidad.
Continuidad sobre un intervalo.

Aprendizajes esperados:

Encontrar en forma aproximada los máximos y mínimos de una función.
Encontrar en forma aproximada los máximos y mínimos de una función.
Determinar algebraica y visualmente las asíntotas de algunas funciones racionales básicas.
Utilizar procesos para la derivación y representan a los objetos derivada y derivada sucesiva como medios adecuados para la predicción local.

Actividad de evaluación:

1.3.1. Estimar el valor del cambio continuo y cambio discreto de un fenómeno, por medio de modelos predictivos.

📣 ACTIVIDAD 3, SEGUNDA EVALUACIÓN. Hacer un resumen en el que des ejemplos de métodos, algunos problemas y sobre todo aplicaciones. Para ello hay que leer el documento de modelospredictivos.pdf que esta en la siguiente liga.

Elabora en un documento de Power Point una presentación de un mínimo de 10 diapositivas, sin contar la portada en la que se agregará una foto de la alumna o alumno, su nombre, carrera que cursa, materia e institución. Enviar el documento vía email a: alejandrotapia.conalepzamora@gmail.com

📌 fecha límite de entrega:6 de mayo.

Modelos predictivos en el futuro

clic aquí para ver video

Productos esperados:

Cálculos y plano cartesiano con interpretación.

¿Qué es el diferencial o la diferencial de una función?

En el ámbito de las matemáticas, se conoce como diferencial a una diferencia muy pequeña de una variable. Un diferencial, en este marco, es la cantidad pequeñísima que se conoce como infinitesimal.

Existen muchas situaciones, dentro y fuera de las matemáticas, en que necesitamos estimar una diferencia, como por ejemplo en las aproximaciones de valores de funciones, en el cálculo de errores al efectuar mediciones (Valor real menos valor aproximado) o simplemente al calcular variaciones de la variable dependiente cuando la variable independiente varía "un poco", etc.

Utilizando a la recta tangente como la mejor aproximación lineal a la función en las cercanías del punto de tangencia, aproximaremos esta DIFERENCIA con la diferencia sobre la recta tangente, a la que llamaremos EL DIFERENCIAL de la función en el punto.

DEFINICION Y EJEMPLOS

Consideremos la siguiente ilustración en donde aproximamos a la función f por su recta tangente.

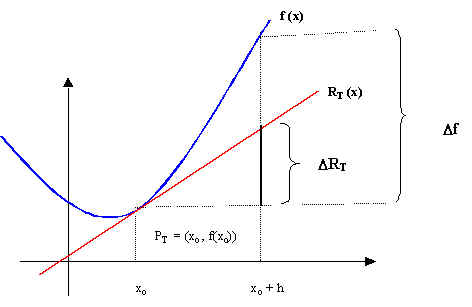
Considerando que la recta tangente es la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia P_T, si le llamamos a la variación de f cuando x varía de x_o a x_o + h y a la variación de la recta tangente en el mismo rango de variación en x, podemos afirmar que para valores de h "cercanos" a 0, estas dos variaciones son muy parecidas, es decir, D f @ D R_T .

Podemos expresar a D R_T en términos de h y el ángulo q que forma la recta tangente con el eje de las abscisas. En el triángulo de la figura, que extraemos a continuación, se observa lo siguiente:

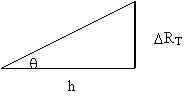
En virtud de que D R_T es un aproximador de la DIFERENCIA D f, lo definiremos como EL DIFERENCIAL DE f en el punto x_o, con respecto al incremento h y lo denotaremos por df, es decir,

df = f '(x_o)h

Observación: El diferencial, en general depende de h y del punto x_o. Por ejemplo el diferencial de f(x) = x² es:

df = f ' (x_o)h = (2x_o)h

que también lo podemos expresar como:

d(x²) = (2x_o)h

Si especificamos el punto x_o, el diferencial dependerá únicamente de h, como se aprecia en los siguientes ejemplos:

a) El diferencial de f(x) = x² en x_o =3 es d(x²) = 6h

b) El diferencial de f(x) = x² en x_o =7 es d(x²) = 14h

c) El diferencial de f(x) = x³ en x_o =2 es d(x³) = 12h

En el caso de la función identidad f(x) = x, como f '(x_o) = 1 para todo x_o, su diferencial nos queda como df = f '(x_o)h = h o bien dx = h

Como h es el diferencial de la función identidad, podemos re-escribir el diferencial de una función f derivable en x_o, como:

df = f '(x_o)dx

Esta expresión nos dice que la variación de una función f es aproximadamente proporcional a la variación de su variable independiente, donde la constante de proporcionalidad es la derivada en el punto en cuestión.

En los siguientes ejemplos estimaremos la variación D f para x_o y h dados y la compararemos con el diferencial.

Ejemplo . Verifique que:

a) Para f(x) = x² se cumple que D f @ df en x_o = 1 y h = 0.1

Solución:

D f = f(1.1) - f(1) = 1.21 - 1 = 0.21
df = f ' (1)dx =(2x|_x=1 )(0.1) = (2)(0.1) = 0.20

La variación real difiere de la aproximada en una centésima.

APLICACIONES DEL DIFERENCIAL

PROBLEMAS DEL TIPO I.

A continuación desarrollaremos algunos ejemplos de aplicación práctica en los que, por medio del diferencial, estimaremos un aumento ó una disminución en alguna función.

Ejemplo 1. Al calentar una placa cuadrada metálica de 15 cm de longitud, su lado aumenta 0.04 cm. ¿Cuánto aumentó aproximadamente su área?.

Solución: Con el fin de ilustrar una situación que se presentará en todos los demás problemas y por la simplicidad de éste en particular, sólo en este caso calcularemos la diferencia de áreas D A y la compararemos con dA.

Nótese que originalmente teníamos una placa de 15 x 15, después de calentarla tenemos la placa de 15.04 x 15.04, como se muestra en la figura.

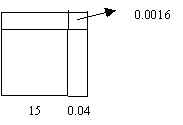
En este caso la función es A(L) = L² y por lo tanto D A en L = 15 y h = 0.04 es:

A(15.004) - A(15) = 226.2016 - 225 = 1.2016

Si ahora calculamos el diferencial de área para A(L) = L² en L = 15 y dL = 0.04, obtenemos:

dA = A' (L)dL = (2L)dL =(2L|_L=15)(0.004) = (30)(0.004) = 1.2

En consecuencia, cuando el lado se incrementa en 0.4 cm, el área aumenta aproximadamente 1.2 cm². (El valor exacto del incremento es 1.2016)

Generalmente este tipo de variaciones se miden en porcentajes, es decir, como 0.04 es el 0.2666% de 15 y 1.2 es el 0.5333% de 225 = (15)², decimos que si el lado de la placa se incrementa en un 0.266%, el área se incrementará aproximadamente en un 0.5333%.

Observación: Si el problema es de una placa metálica del mismo tamaño que se enfría 0.04 cm, entonces h = -0.04 y el diferencial resultaría el mismo sólo que con signo contrario, es decir dA = -1.2. Como estamos usando la recta tangente para estimar la diferencia, la linealidad hace que el cateto opuesto en ambos triángulos de la figura, sean iguales

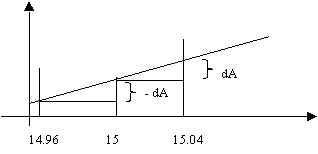
Resolvamos ahora el mismo problema con otros datos expresados porcentualmente

Ejemplo 2. Al enfriar una placa cuadrada metálica de 20 cm de longitud, su lado disminuye un 0.03%. ¿Cuánto disminuirá porcentualmente su área?.

Solución: El 0.03% de 20 es , por lo que en este caso:

A(L) = L² , L_o = 20 y dL = -0.006

D A @ dA = 2LdL = 2(20)(-0.006) = (40)(-0.006) = -0.24

Podemos calcular que 0.24 representa el 0.06% de (20)², por lo que, cuando el lado disminuye un 0.03%, el área disminuye aproximadamente un 0.06%, es decir se duplica porcentualmente.

Este último resultado lo podemos obtener directamente de la siguiente manera:

D A @ dA = 2LdL = 2(20)[] =