mensaje del docente clase 2 de marzo
si no puedes ver el video da clic aquí
material didáctico de apoyo
Operaciones aritméticas con funciones
Objetivos de aprendizaje
· Dadas dos funciones, f y g, encontrar su suma, f + g.
· Dadas dos funciones, f y g, encontrar su resta, f – g.
· Dadas dos funciones, f y g, encontrar su producto, f • g.
· Dadas dos funciones, f y g, encontrar su cociente, f/g.
Introducción
Estás acostumbrado a sumar, restar, multiplicar y dividir números reales, haces estas operaciones todos los días en una variedad de situaciones. También has aprendido cómo realizar estas cuatro operaciones básicas en expresiones algebraicas. Entonces, aunque no necesitas calcular ![]() muy a menudo, sabes cómo hacerlo.
muy a menudo, sabes cómo hacerlo.
Si sabes cómo realizar las cuatro operaciones básicas en polinomios, entonces también puedes sumar, restar, multiplicar y dividir funciones. La notación se verá diferente al principio, pero aprender un par de pasos te puede ayudar a llegar a la respuesta correcta.
Entendiendo la notación
Una función es una correspondencia entre dos conjuntos: el dominio y el rango. Además de evaluar funciones, puedes hacer operaciones con funciones.
Digamos que trabajas con las siguientes dos funciones.
![]()
La suma de las funciones puede escribirse como f(x) + g(x) o (f + g)(x). Observa lo que sucede cuando se suman estas dos funciones.
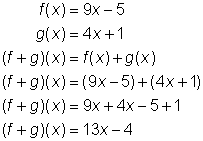
Y es todo, la suma de las dos funciones es la suma de los dos polinomios.
La suma, la resta, la multiplicación y la división se explicarán también. La tabla siguiente muestra la notación usada para cada tipo de operación aritmética.
Suma |
|
|
Resta |
|
|
Multiplicación |
|
|
División |
|
|
Ya viste un ejemplo de sumar dos funciones. Veamos otro ejemplo. El dominio (los valores de x) para ambas funciones es todos los números reales.
Ejemplo | ||
Problema |
Encontrar (f + g)(x). |
|
|
| Identifica f(x) y g(x). Reemplaza f(x) con |
Respuesta |
|
|
La resta sigue el mismo proceso. Siempre y cuando te acuerdes de cómo restar un polinomio de otro, puedes restar una función de otra.
Ejemplo | ||
Problema |
Encontrar (g – f)(x). |
|
|
| Reemplaza g(x) y f(x) con sus respectivas expresiones.
Luego suma y combina los términos semejantes. |
Respuesta |
|
|
Ejemplo | ||
Problema |
Encontrar (f – h)(x). |
|
|
| Observa que (f – h)(x) = f(x) – h(x).
Puedes ignorar g(x) porque no se requiere resolver para este problema.
Reemplaza las notaciones de función con sus polinomios apropiados y resta. |
Respuesta |
|
|
A) B) C) D)
|
Multiplicar y dividir funciones también es como multiplicar y dividir polinomios. Revisa los siguientes ejemplos.
Ejemplo | ||
Problema |
Encontrar el producto de f y g. |
|
|
| Para encontrar el producto, multiplica las funciones. |
|
| Reemplaza f(x) con (2x + 1) y g(x) con (5x – 3). |
Respuesta |
|
|
Ejemplo | ||
Problema |
Encontrar |
|
|
| Para encontrar el cociente, divide f entre g. Sustituye los polinomios por f(x) y g(x) y divide. Sumamos Recuerda renombrar |
Respuesta |
|
|
Las operaciones con tres funciones trabajan de la misma forma. En el ejemplo siguiente, dos funciones se suman y luego se dividen entre una tercera función. No es distinto de lo que ya has hecho con polinomios, sólo no dejes de sustituir los polinomios en las funciones correctas, combina, divide y simplifica.
Ejemplo | |||
Problema |
Encontrar |
| |
| Reemplaza f(x), g(x) y h(x) con polinomios equivalentes. Sumamos | ||
| Suma f(x) y g(x). | ||
| Divide entre h(x). Saca el factor de 3x2 del numerador y luego simplifica la expresión, usando | ||
Respuesta |
|
| |
MODELADO DE FUNCIONES
- Encontrar un problema del mundo real.
- Formular un modelo matemático acerca del problema, identificando variables (dependientes e independientes) y estableciendo hipótesis lo suficientemente simples para tratarse de manera matemática.
- Aplicar los conocimientos matemáticos que se posee para llegar a conclusiones matemáticas.
- Comparar los datos obtenidos como predicciones con datos reales. Si los datos son diferentes, se reinicia el proceso.
- Para conseguir las funciones primero se establecen las variables, luego se procede a traducir del lenguaje común al lenguaje matemático, para finalmente expresar la variable dependiente en términos o en función de la variable independiente.

📌 ACTIVIDAD 3. RESOLUCIÓN DE PROBLEMAS
En tu cuaderno utilizando diferentes tipos de tintas para resaltar títulos o temas y contendido, REALIZAR los problemas planteados a continuación indicando cómo se resolvieron dichos problemas, es decir poner que formula o formulas o ecuaciones matemáticas se utilizaron.
👉 EVIDENCIA A RECOPILAR. Imágenes o fotos de tus problemas, recuerda todo pasarlo a un documento de Word, colocar una portada con tu nombre, grupo, asignatura, número de evidencia y unidad. Enviar vía Facebook o correo electrónico al docente tan pronto lo tengas.
PROBLEMA 1:
Se va a construir una caja rectangular sin tapa a partir de una lámina metálica de 30 cm de largo por 20 cm de ancho. Para ello se van a recortar cuadrados de lado "x" en las esquinas y luego se van a doblar los lados hacia arriba.
🎯Expresar el volumen (V) de la caja como función de (x)
clave/tip, te dejo gran parte de la pista de cómo resolver este problema. tu completa mediante sustituir los valores de "x" y realizar las operaciones correspondientes para hallar el valor de "V"
PROBLEMA 2:
Una huerta de manzanos tiene 40 arboles por hectárea y el promedio de producción es de 300 manzanas por árbol por año.
Si por cada árbol que se plante por hectárea, además de los 40, la producción promedio disminuye en 5 manzanas.
🎯Expresar la producción(P) en función de las manzanas(x)
PROBLEMA 3:
Se va a construir una caja rectangular abierta con una base cuadrada de longitud x y un volumen de 16,000 cm cúbicos.
🎯Expresar la área(A) de la caja en función su longitud(x)
clave/tip, te dejo gran parte de la pista de cómo resolver este problema, tu completa sustituyendo el valor de "x" e "y", y realiza las operaciones correspondientes para hallar el valor de "A"

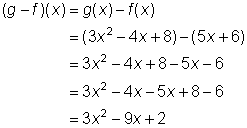

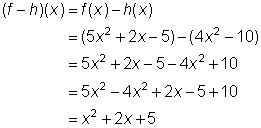








No hay comentarios.:
Publicar un comentario