Análisis Derivativo de Funciones

📴si abres este blog desde un dispositivo móvil y no puedes visualizar videos o imágenes requieres abrir en versión web para ello ve hasta el final de cada página y aparecerá abajo del botón de página principal la opción "Ver la versión Web" da clic ahí y listo.

📌no olvides checar tu asistencia ingresando a la pagina de horario-asistencia

Propósito del módulo:

Determina la derivada de una función en un punto correspondiente al valor de la tasa de variación instantánea en ese punto, para resolver situaciones de la vida personal y profesional.

📑 DESCARGAR GUIA PEDAGOGICA Y DE EVALUACIÓN

clic aquí

MENSAJE DEL DOCENTE

UNIDAD 1: 1. Aplicación de la derivada con estrategias variacionales.

1.1 Determina la razón del cambio de una variable y lo representa en tablas y gráficas.

A. Determinación de elementos de funciones.

Definición de función y relación.
Dominio y rango
Gráfica de funciones
Raíces
Intervalos de crecimiento

B. Clasificación de funciones.

Constante
Lineal
Cuadrática
Polinomial
Racional
Valor absoluto
Escalonada
Algebraicas
Transcendentes
Trigonométricas

C. Cálculo con funciones.

Suma
Resta
Multiplicación
División
Potenciación
Composición de funciones
Funciones inversas

D. Modelación de funciones.

Determinación del modelo matemático
Resultados o solución

📌 INDICACIONES DEL DOCENTE ACTIVIDADES 1 Y 2

📌 ACTIVIDAD 1. TOMA DE APUNTES

En tu cuaderno utilizando diferentes tipos de tintas para resaltar títulos o temas y contendido, incluir conceptos que se presenta en la sección A del subtema 1.1 (función y relación; Dominio y rango; Raíces; Intervalos de crecimiento) GRAFICANDO algunos ejemplos de estas para afianzar tu comprensión.

👉 EVIDENCIA A RECOPILAR. Imágenes o fotos de tus apuntes, recuerda todo pasarlo a un documento de Word, colocar una portada con tu nombre, grupo, asignatura, número de evidencia y unidad. Enviar vía Facebook o correo electrónico al docente tan pronto lo tengas.

---

Introducción

A nuestro alrededor encontramos cosas que se relacionan entre sí, o que están en función de algún parámetro, por ejemplo el peso y la altura, la masa corporal en función del peso y la estatura, los kilómetros recorridos y la cantidad de gasolina consumida, y muchos ejemplos más.

Al alemán Johann Dirichlet (1805-1859), se le atribuye la definición moderna de función como una regla de correspondencia entre dos conjuntos.

Las funciones pueden ser representadas mediante gráficas, así como llevar a cabo operaciones entre ellas y ser utilizadas para describir situaciones o fenómenos que se presentan a diario en nuestro entorno mediante la modelación matemática.

Definición de una función en matemáticas

Una función es una relación o correspondencia entre dos magnitudes, de manera que a cada valor de la primera le corresponde un único valor de la segunda (o ninguno), que llamamos imagen o transformado. A la función se le suele designar por f y a la imagen por f(x), siendo x la variable independiente.

Fig. 1 ejemplo de funciones

ejemplo resuelto de funciones lineales

si no puedes ver el video da clic aquí

Definición de una relación en matemáticas

La relación matemática es el vínculo que existe entre los elementos de un subconjunto con respecto al producto de dos conjuntos. Una función implica la operación matemática para determinar el valor de una variable dependiente según el valor de una variable independiente. Toda función es una relación pero no toda relación es una función.

Cuando hablamos de una función matemática de un conjunto A en un conjunto B nos referimos a una regla o mecanismo que relaciona los elementos del conjunto A con un elemento del conjunto B.

Concepto de función

"Sean x y y dos variables reales, se dice entonces que y es función de x si a cada valor que tome x le corresponde un valor de y."
La variable independiente es la x mientras que y es la variable dependiente o función:
y=ƒ(x)
El conjunto en que varía la x se denomina dominio de la función (original) y el de la variación de y rango de la función (imagen).
El conjunto de pares (x, y) tales que y=ƒ(x) se denomina grafo de la función; si se representan en unos ejes cartesianos se obtiene una familia de puntos que se denomina gráfica de la función.

VIDEO EXPLICATIVO DE FUNCIONES Y RELACIONES

si no puedes ver el video da clic aquí

Dominio y rango de una función

El dominio de una función f ( x ) es el conjunto de todos los valores para los cuales la función está definida, y el rango de la función es el conjunto de todos los valores que f toma.
(En gramática, probablemente le llame al dominio el conjunto reemplazo y al rango el conjunto solución. Quizá también estos han sido llamados la entrada y salida de la función.)
Ejemplo 1:
Considere la función mostrada en el diagrama.
Aquí, el dominio es el conjunto { A , B , C , E }. D no está en el dominio, ya que la función no está definida para D .
El rango es el conjunto {1, 3, 4}. 2 no está en el rango, ya que no hay letra en el dominio que se enlace con el 2.
Ejemplo 2:
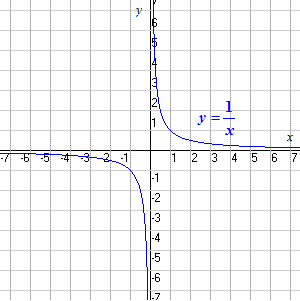
El dominio de la función
f ( x ) = 1/ x
es todos los números reales excepto el cero (ya que en x = 0, la función no está definida: la división entre cero no está permitida!).
El rango también es todos los números reales excepto el cero. Puede ver que hay algún punto en la curva para cada valor de y excepto para y = 0.
Ejemplo 3:
La notación siguiente muestra que el dominio de la función está restringido al intervalo (–1, 1).
f ( x ) = x 2 , –1 x 1
La gráfica de esta función es como se muestra. Dese cuenta de los círculos abiertos, que muestran que la función no está definida en x = –1 y x = 1. Los valores del rango de y desde 0 hasta el 1 (incluyendo el 0, pero no incluyendo el 1). Así el rango de la función es
0 y < 1.

VIDEO DE CÓMO SE GRAFICA UNA FUNCIÓN

VIDEO 1

si no puedes ver el video da clic aquí

VIDEO 2

si no puedes ver el video da clic aquí

Raíz de una función lineal

La raíz (x₁) de una función lineal es el valor de x que se corresponde con el valor de ordenada cero, es decir, (x₁, 0). ... Ejercicio: Calcular la raíz, indicar la ordenada al origen y pendiente de la recta: y = 3x+6.