1.2 Analiza la razón del cambio de la variable, de acuerdo con los patrones establecidos en el movimiento lineal.
A. Cálculo de límites de funciones
- Noción intuitiva de límite y límites laterales
- Teorema de los límites
- Límites de funciones determinados e indeterminados:
- Límites unilaterales
- Límites al infinito
- Límites en infinito
B. Determina razones de cambio.
- La recta Normal y la pendiente de la recta tangente a una curva en un punto
- Relación entre los incrementos de la función y la variable independiente
- La función de posición y la velocidad
Diversas formas de ver un límite que no son propiamente matemáticas
Un límite puede entenderse como una línea real o imaginaria que separa dos espacios (casas, ciudades, terrenos, etc).
No, el límite que aprenderemos a determinar hoy no siempre es una línea, más bien es un valor (cuando existe).
Un límite puede verse como el final o el extremo de algo (fecha límite, límite del estacionamiento, límite de la paciencia, etc.).
No, nuestro límite no siempre es el final de algo.
Un límite puede verse como una restricción (límite de velocidad, límite de ocupantes en un elevador).
No, al determinar un límite como los que veremos hoy no obtenemos un valor como esos, que restringen pero pueden no respetarse.
¿Qué es entonces un límite en matemáticas?
Existen diversas formas de entender los límites en matemáticas:
Límite de una sucesión:
Es el número al que se van acercando los términos de una sucesión. Puede o no existir. Escribiré sobre eso en otra ocasión.
Límite de una función:
Es el valor al que tiende la función cuando la variable independiente tiende a un valor dado, sin tomar ese valor.
Forma de determinar diferente a la usada en otros contextos
Una razón de la dificultad para comprender este tema es que el determinar un límite implica revisar qué ocurre al acercarse a un valor por ambos lados, lo cual no es tan fácil de relacionar con los conceptos de límite que normalmente manejamos, como un límite de capacidad de un contenedor, por ejemplo. Si lo excedes, se tira lo que estés agregando. El límite en cálculo es diferente.
Toda Función puede ser representada, dibujada, y así podremos observar lo que le ocurre en un punto de esa curva, y en sus proximidades. Pero esta representación no es nada fácil en cuanto la función sea compleja, y más si es en tres o más dimensiones.
Pero el Análisis Infinitesimal, con los Límites de funciones, nos da una herramienta práctica y precisa, para saber lo anterior, sin realizar la representación de la función. Es como en medicina interna, se hace un diagnóstico a través de la realización de un Análisis de sangre u orina, sin observar mediante imagen.
Realmente tenemos cuatro tipos de límites de funciones, a saber:
1) Límite de una función en un punto lim f(x) = l, nº real, cuando x tiende, se aproxima a un punto.
2) Límite finito en el infinito lim f(x) = l, cuando x tiende a infinito.
3) Límite infinito en el infinito lim f(x) = infinito, cuando x tiende a infinito.
4) Límite infinito cuando x tiende a un punto lim f(x) = infinito, cuando x tiende a un punto.
Para calcular un límite de una función, lo primero que se hace es sustituir el número o el infinito en la función. Nos puede dar un número, o una Indeterminación, algo desconocido.
Así lim 4x - 3 cuando x tiende a 2, es 5, pues al sustituir tenemos 4.2 - 3 = 8 - 3 = 5
lim 5x + 2 cuando x tiende a cero, es 2 , pues al sustituir tenemos 5.0 + 2 = 0 + 2 = 2.
Por tanto que quede claro que los Límites de funciones son una herramienta matemática, que nos hace averiguar lo que le ocurre a la función en las proximidades de puntos o el infinito, y todo sin ver, representar, la función
Notación (forma de escribir un límite)
El límite de la función f(x) cuando x tiende a a, es L. Se escribe:
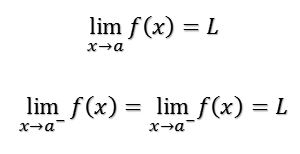
fuente de consulta: impulso matemático
Concepto de límites
Limites Laterales
Concepto de límites laterales
A la izquierda, en 1, concepto y notación del límite por la izquierda. Observa que, a medida que tomamos valores próximos a a, pero menores que este (fondo verde claro), los correspondientes valores de f(x), en rojo, se aproximan a Li. Decimos que Li es el valor del límite de la función cuando x se aproxima a a por la izquierda.
En 2, el concepto y notación del límite por la derecha. A medida que tomamos valores próximos a a, pero mayores que este (fondo verde oscuro), los correspondientes valores de f(x) se aproximan a Ld. Decimos que Ld es el valor del límite de la función cuando x se aproxima a a por la derecha.
Límite por la izquierda
El valor del límite de una función f(x) cuando x tiende a a por la izquierda es el valor al que se acerca y=f(x) cuando x se acerca a a tomando valores menores que a. Pueden darse los siguientes casos.
Límite por la izquierda de una función
En 1 te presentamos la notación utilizada para referirnos al límite por la izquierda de una función. En 2, 3 y 4 tenemos tres casos concretos que pueden darse.
En 2 el límite por la izquierda es una valor real concreto, L. Observa como el valor del límite no tiene porqué coincidir con el de la función en el punto.
En 3, el límite por la izquierda es infinito, y por tanto, a medida que nos aproximamos a a la función crece indefinidamente.
En 4, el caso complementario, el límite por la izquierda es menos infinito.
En la definición de límite de una función en un punto decíamos que era el valor al que se aproximaba la función f(x) cuando la x se acercaba a a. Pero a a, siempre que sea un valor finito, podemos acercarnos por la izquierda, esto es, tomando valores menores que a, o por la derecha, es decir, tomando valores mayores que a. Los límites laterales contemplen precisamente estas dos posibilidades.
Límite por la derecha
El valor del límite de una función f(x) cuando x tiende a a por la derecha es el valor al que se acerca y=f(x) cuando x se acerca a a tomando valores mayores que a. Pueden darse los siguientes casos.
Límite por la derecha de una función
En 1 te presentamos la notación utilizada para referirnos al límite por la derecha de una función.
En 2, 3 y 4 tenemos tres casos concretos que pueden darse.
En 2 el límite por la derecha es una valor real concreto, L.
En 3, el límite por la derecha es infinito, y por tanto, a medida que nos aproximamos a a la función crece indefinidamente.
En 4, el caso complementario, el límite por la derecha es menos infinito.
Límite infinito
Decimos que ellímite de una función cuando x se aproxima a a por la izquierda es infinito cuando para cualquier valor k (en el eje y), tan grande como se quiera, siempre se puede encontrar un valor real positivo δ (en el eje x) tal que las imágenes de cualquier x comprendido entre a-δ y a serán siempre mayores que k.
Decimos que
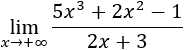
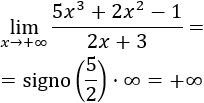
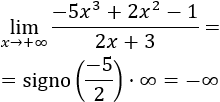
No hay comentarios.:
Publicar un comentario